Выпуклый N-угольник на параболе: олимпиадная задача по планиметрии для 10–11 класса

  а) Пусть O – вершина параболы. Отложим на правой ветви 1005 равных хорд  OA₁, A₁A₂, A₂A₃, ..., A₁₀₀₄A₁₀₀₅  длины t. Рассмотрим ломаную OB₁B₂...B₁₀₀₅, симметричную OA₁A₂...A₁₀₀₅ относительно оси параболы. Очевидно, длина l(t) отрезка B₁₀₀₅A₁₀₀₅ непрерывно зависит от t. При 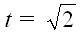    B₁A₁ = 2 > t,  тем более  l(t) > t.  При  t = 4020  ордината точки A₁₀₀₅ меньше  1005·4020 = 2010²,  значит, её абсцисса меньше 2010, и  l(t) < 2·2010 = t.  По теореме о промежуточном значении найдётся t, при котором  l(t) = t.  В этом случае многоугольник OA₁A₂...A₁₀₀₅B₁₀₀₅...B₁ равносторонний.   б) Лемма. Если в выпуклом четырёхугольнике две противоположные стороны равны, то в другой паре противоположных сторон меньше та, сумма углов при которой больше.

  Доказательство. Пусть в четырёхугольнике ABCD сумма углов A и B больше 180° и  AD = BC.  Построим параллелограмм ABCE. Треугольник CAD получается из треугольника CAE увеличением угла A, поэтому  CD > CE = AD.   Следствие. Пусть четырёхугольник ABCD вписан в параболу,  AD = BC,  а точки A и B лежат на дуге CD параболы. Тогда  CD > AB.

  Доказательство. Ясно, что четырёхугольник ABCD – часть сегмента параболы, отсечённого хордой CD. Пусть касательные к параболе в точках C и D пересекаются в точке M. Треугольник CMD содержит упомянутый сегмент, а, значит, и четырёхугольник ABCD. Поэтому

∠BCD + ∠ADC < ∠MCD + ∠MDC < 180°.   Решение задачи. Пусть нашёлся такой 2012-угольник. Занумеруем его вершины в порядке возрастания абсцисс от A₁ до A₂₀₁₂ (в этом же порядке они будут появляться при обходе 2012-угольника против часовой стрелки). Применяя 1005 раз вышеприведённое следствие, последовательно получим

A₁A₂₀₁₂ > A₂A₂₀₁₁ > ...

A₁₀₀₆A₁₀₀₇.   Противоречие.

а) Существует;  б) не существует.