Олимпиадная задача: Центр окружности треугольника PQC и вписанная окружность ABC
Задача
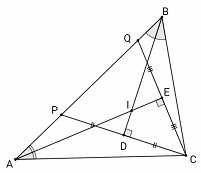
На наибольшей стороне AB треугольника ABC взяли такие точки P и Q, что AQ = AC, BP = BC.
Докажите, что центр описанной окружности треугольника PQC совпадает с центром вписанной окружности треугольника ABC.
Решение
Треугольник BPC – равнобедренный, поэтому биссектриса угла B совпадает с серединным перпендикуляром к стороне CP. Аналогично биссектриса угла A совпадает с серединным перпендикуляром к отрезку CQ. Но центр вписанной окружности треугольника ABC лежит на пересечении упомянутых биссектрис, а центр описанной окружности треугольника PQC – на пересечении упомянутых серединных перпендикуляров.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет