Олимпиадная задача по планиметрии: найти MN в треугольнике ABC с медианой
Задача
В треугольникеABCизвестно, чтоAB= 10,BC= 24, а медианаBDравна 13. Окружности, вписанные в треугольникиABDиBDCкасаются медианыBDв точкахMиNсоответственно. НайдитеMN.
Решение
Докажем сначала следующее утверждение. Если в треугольник XYZ вписана окружность, а x – расстояние от вершины X до касания окружности со стороной XY и YZ = a, то x = p – a, где p – полупериметр треугольника.Обозначим точки касания вписанной окружности со сторонами XY, YZ и XZ через Z1, X1 и Y1 соответственно. Пусть XZ = b и XY = c. Тогда
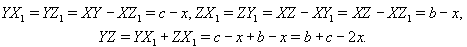
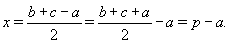
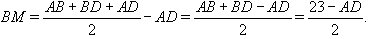
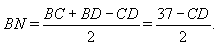
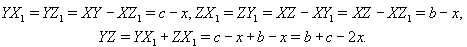
Ответ
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет