Олимпиадная задача по планиметрии: найдите площадь трапеции с вписанной окружностью
Задача
Окружность, вписанная в равнобедренную трапецию, делит её боковую сторону на отрезки, равные 4 и 9. Найдите площадь трапеции.
Решение
Пусть окружность с центром O и радиусом r, вписанная в равнобедренную трапецию ABCD, касается оснований AD и BC в точках K и L соответственно, а боковой стороны CD – в точке M. При этом CM = 4, DM = 9.Поскольку CO и DO – биссектрисы углов BCD и ADC, сумма которых равна 180°, угол COD – прямой, поэтому OM – высота прямоугольного треугольника COD, проведённая из вершины прямого угла. Следовательно,
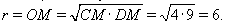
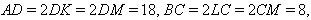

Ответ
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет