Олимпиадная задача по планиметрии для 8-10 класса: отрезок MN в трапеции
Задача
Точки M и N расположены на боковых сторонах соответственно AB и CD трапеции ABCD, причём MN || AD. Известно, что площадь трапеции MBCN относится к площади трапеции AMND как 2 : 3. Найдите MN, если BC = a, AD = b.
Решение
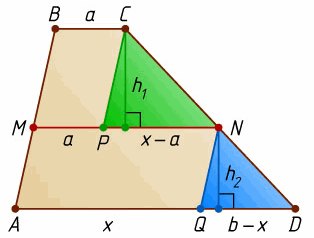
Первый способ. Пусть P – точка пересечения с MN прямой, проходящей через точку C параллельно AB, Q – точка пересечения с AD прямой, проходящей через точку N параллельно AB. Обозначим MN = x; h1 и h2 – высоты подобных треугольников PCN и QND (см. рис. слева).
Пусть b > a. Отношение площадей трапеций BMNC и MADN равно 2 : 3, поэтому 3(x + a)h1 = 2(b + x)h2, откуда
.
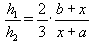Из подобия треугольников CPN и NQD следует, что
.
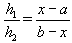Поэтому 
.
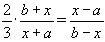Отсюда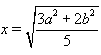 
.
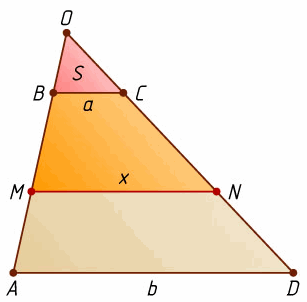
MN = x – искомый отрезок. Тогда 3(SMNO – S) = 2(SAOD – SMNO), или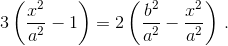 
Отсюда x² = ½ (3a² + 2b²).
Ответ
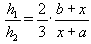
Чтобы оставлять комментарии, войдите или зарегистрируйтесь