Олимпиадная задача по планиметрии: площадь шестиугольника в четырёхугольнике
Задача
На сторонах AB, BC, CD и AD выпуклого четырёхугольника ABCD расположены точки M, N, K и L соответственно, причём AM : MB = 3 : 2, CN : NB = 2 : 3, CK = KD и AL : LD = 1 : 2. Найдите отношение площади шестиугольника MBNKDL к площади четырёхугольника ABCD.
Решение
Проведём диагональ BD четырёхугольника ABCD. Тогда
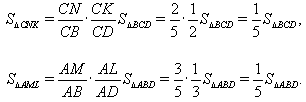
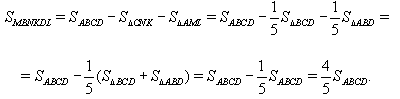
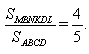
Ответ
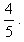
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет