Олимпиадная задача по планиметрии для 8–10 классов: площадь CKOL в треугольнике
Задача
В треугольнике ABC известны стороны BC = a, AC = b, AB = c и площадь S. Биссектрисы BL и AK пересекаются в точке O. Найдите площадь четырёхугольника CKOL.
Решение
Биссектриса треугольника делит его сторону на отрезки, пропорциональные двум другим сторонам, т.е.
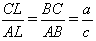, а т.к. AC = b, то
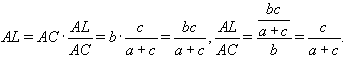
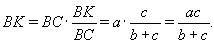
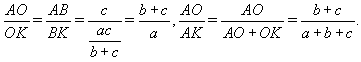
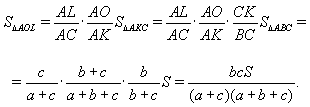
Ответ
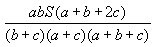
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет