Олимпиадная задача по планиметрии для 8–10 классов: площади треугольников
Задача
На сторонах BC, AC и AB треугольника ABC расположены точки A1, B1 и C1 соответственно, причём BA1 : A1C = CB1 : B1A = AC1 : C1B = 2 : 3. Найдите площадь треугольника, образованного пересечениями прямых AA1, BB1 и CC1, если известно, что площадь треугольника ABC равна 1.
Решение
Пусть K – точка пересечения отрезков
BB1 и CC1. Через точку
B проведём прямую, параллельную AC, и продолжим CC1
до пересечения с этой прямой в точке T. Положим CB1 = 2a,
AB1 = 3a. Треугольники BC1T и
AC1C подобны с коэффициентом
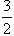 .
Поэтому
.
Поэтому  ,
а из подобия треугольников BKT и B1KC находим, что
,
а из подобия треугольников BKT и B1KC находим, что


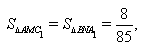
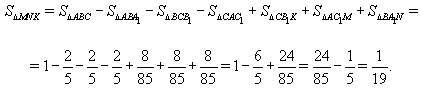
Ответ
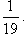
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет