Олимпиадная задача: площадь треугольника по основаниям высот (Планиметрия, 8-10 классы)

  Пусть H – точка пересечения высот треугольника ABC; A₂, B₂, C₂ – точки пересечения продолжений высот AA₁, BB₁, CC₁ соответственно с описанной окружностью Ω треугольника ABC. Тогда A₁, B₁, C₁ – середины отрезков HA₂, HB₂, HC₂ (см. задачу 155463). Значит, A₁B₁, B₁C₁, A₁C₁ – средние линии треугольников A₂HB₂, B₂HC₂, A₂HC₂, поэтому стороны треугольника A₂B₂C₂ соответственно параллельны сторонами треугольника A₁B₁C₁. Следовательно, треугольник A₂B₂C₂ подобен треугольнику A₁B₁C₁ с коэффициентом 2. Поэтому  A₂B₂ = 2A₁B₁ = 26,  B₂C₂ = 2B₁C₁ = 28,

A₂C₂ = 2A₁C₁ = 30.

  Пусть O – центр Ω, R – её радиус. Обозначим  ∠A₂B₂C₂ = ∠A₁B₁C₁ = β.  Из треугольника A₁B₁C₁ по теореме косинусов находим, что  

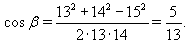
  Значит, 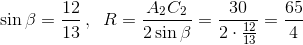    (поскольку Ω – описанная окружность треугольника A₂B₂C₂).

  Радиусы OA₂, OB₂, OC₂ перпендикулярны отрезкам B₁C₁, A₁C₁, A₁B₁ соответственно (см. решение задачи 216334). Следовательно,

S_ABC = S_AB1OC1 + S_BA1OC1 + S_CA1OB1 = ½ B₁C₁·OA + ½ A₁C₁·OB + ½ A₁B₁·OC = ½ (B₁C₁ + A₁C₁ + A₁B₁)R = ½ (14 + 15 + 16)·⁶⁴/₄ = ¹³⁶⁵/₄.

¹³⁶⁵/₄.