Олимпиадная задача по стереометрии для 10–11 класса: сфера вписана в четырёхугольную пирамиду
Задача
Дана четырёхугольная пирамида, в которую можно вписать сферу, причём центр этой сферы лежит на высоте пирамиды. Докажите, что в основания пирамиды можно вписать окружность.
Решение
Пусть SH — высота четырёхугольной пирамиды SABCD с вершиной S , O — центр сферы, вписанной в пирамиду ( O лежит на отрезке SH ), K , L , M и N — точки касания сферы с гранями ASB , BSC , CSD и ASD соответственно. Прямоугольные треугольники OKS , OLS , OMS и ONS равны по катету (радиус сферы) и гипотенузе, поэтому
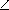 OSK =
OSK =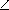 OSL=
OSL=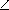 OSM=
OSM=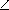 OSN.
OSN.
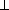 SK1.
Аналогично, BC
SK1.
Аналогично, BC 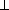 SL1, CD
SL1, CD 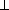 SM1и AD
SM1и AD 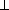 SN1,
а также HK1
SN1,
а также HK1 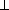 AB , HL1
AB , HL1 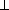 BC , HM1
BC , HM1 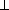 CD и HN1
CD и HN1 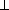 AD .
Прямоугольные треугольники SK1H , SL1H , SM1H и SN1H равны по катету и прилежащему острому углу, поэтому HK1=HL1=HM1=HN1, значит, точка H равноудалена от сторон
четырёхугольника ABCD . Следовательно, H — центр окружности,
вписанной в этот четырёхугольник.
AD .
Прямоугольные треугольники SK1H , SL1H , SM1H и SN1H равны по катету и прилежащему острому углу, поэтому HK1=HL1=HM1=HN1, значит, точка H равноудалена от сторон
четырёхугольника ABCD . Следовательно, H — центр окружности,
вписанной в этот четырёхугольник.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет