Олимпиадная задача по стереометрии для 10-11 классов: объём треугольной пирамиды с равными гранями
Задача
Все грани треугольной пирамиды — равные равнобедренные треугольники, а высота пирамиды совпадает с высотой одной из её боковых граней. Найдите объём пирамиды, если расстояние между наибольшими противоположными ребрами равно 1.
Решение
Пусть высота DH пирамиды ABCD с вершиной D является высотой
боковой грани ADC . Предположим (рис.1), что AC=AD=b , CD=a ( a 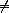 b ,
т.к. в противном случае ABCD — правильный тетраэдр). Тогда
из равенства всех граней пирамиды следует, что BD=BC=b и
высота равнобедренного треугольника BCD , опущенная на боковую
сторону BC , равна высоте DH равнобедренного треугольника ACD , опущенной на боковую сторону AC , что невозможно,
т.к. DH — перпендикуляр к плоскости основания пирамиды,
а DP — наклонная к этой плоскости. Таким образом, DH —
высота равнобедренного треугольника ADC , опущенная на основание.
Обозначим DA=DC=a , AC=b (рис.2). Тогда AB=BC=a и BD=AC=b .
По теореме Пифагора
b ,
т.к. в противном случае ABCD — правильный тетраэдр). Тогда
из равенства всех граней пирамиды следует, что BD=BC=b и
высота равнобедренного треугольника BCD , опущенная на боковую
сторону BC , равна высоте DH равнобедренного треугольника ACD , опущенной на боковую сторону AC , что невозможно,
т.к. DH — перпендикуляр к плоскости основания пирамиды,
а DP — наклонная к этой плоскости. Таким образом, DH —
высота равнобедренного треугольника ADC , опущенная на основание.
Обозначим DA=DC=a , AC=b (рис.2). Тогда AB=BC=a и BD=AC=b .
По теореме Пифагора
BH=DH=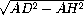 =
=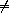 ,
,
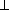 BH , то
BH , то
b=BD=BH· 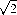 =
=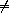 ·
· 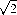 =
=
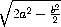 .
.
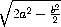 находим, что b2=
находим, что b2=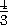 a2. Следовательно, b>a , значит, расстояние
между наибольшими противоположными рёбрами — это расстояние между AC и BD .
Пусть M — середина BD . Тогда HM — высота и медиана
равнобедренного треугольника BHD , а т.к. HM лежит в плоскости,
перпендикуляной AC , то HM — общий перпендикуляр прямых BD и AC , HM=
a2. Следовательно, b>a , значит, расстояние
между наибольшими противоположными рёбрами — это расстояние между AC и BD .
Пусть M — середина BD . Тогда HM — высота и медиана
равнобедренного треугольника BHD , а т.к. HM лежит в плоскости,
перпендикуляной AC , то HM — общий перпендикуляр прямых BD и AC , HM=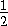 BD=
BD=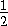 b . По условию
задачи HM=1, значит, b=2. Тогда
b . По условию
задачи HM=1, значит, b=2. Тогда
a=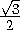 b=
b=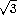 ,
DH=BH=MH
,
DH=BH=MH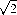 =
=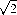 .
.
VABCD=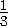 SΔ ABC· DH=
SΔ ABC· DH=
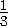 ·
· 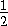 AC· BH· DH=
AC· BH· DH=
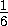 ·
· 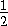 · 2 ·
· 2 · 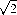 ·
· 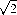 =
=
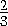 .
.
Ответ
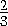 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь