Олимпиадная задача по стереометрии: площадь сечения пирамиды TABC через середины рёбер
Задача
Сторона основания ABC пирамиды TABC равна 4, боковое
ребро TA перпендикулярно плоскости основания. Найдите
площадь сечения пирамиды плоскостью, проходящей через
середины рёбер AC и BT параллельно медиане BD грани BCT , если известно, что расстояние от вершины T до этой плоскости равно 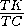 .
.
Решение
Плоскость грани BCT проходит через прямую BD , параллельную
секущей плоскости, значит, она пересекает секущую плоскость по
прямой, проходящей через середину N ребра BT парараллельно BD . Эта прямая пересекает ребро CT в его середине K , поэтому 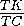 =
=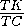 .
.
Пусть прямая, проходящая через середину M ребра AC и точку K , пересекает прямую AT в точке P , а прямая PN пересекает
ребро AB в точке L . Тогда четырёхугольник MKNL — сечение,
о котором говорится в условии задачи.
По теореме Менелая 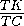 ·
· 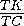 ·
· 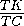 =1,
или
=1,
или 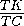 ·
· 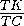 ·
· 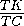 =1, откуда
=1, откуда 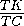 =
=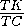 .
Аналогично,
.
Аналогично, 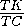 ·
· 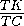 ·
· 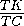 =1, или
=1, или 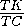 ·
· 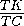 ·
· 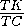 =1, откуда
=1, откуда 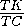 =3.
Пусть K1и N1— ортогональные проекции точек K и N на плоскость основания ABC . Тогда MK1N1L — ортогональная
проекция сечения MKLN на плоскость основания. Если SMKLN = S ,
а SMK1LN1=s , то S=
=3.
Пусть K1и N1— ортогональные проекции точек K и N на плоскость основания ABC . Тогда MK1N1L — ортогональная
проекция сечения MKLN на плоскость основания. Если SMKLN = S ,
а SMK1LN1=s , то S=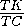 , где α —
угол между плоскостями сечения и основания пирамиды.
Известно, что
, где α —
угол между плоскостями сечения и основания пирамиды.
Известно, что
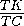 =
=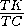 ,
,
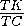 =
=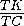 ,
, 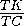 =
=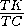 =
=
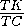 ,
, 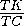 =
=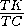 =
=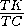 ,
,
s=SΔ AML-SΔ AK1N1 =
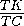 ·
· 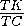 SΔ ABC-
SΔ ABC-
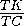 ·
· 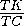 SΔ ABC=
SΔ ABC=
=(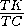 ·
· 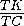 -
-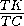 ·
· 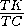 )
)
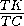 =
=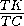 · 4
· 4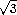 =
=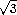 .
.
Пусть AE — перпендикуляр, опущенный из точки A на ML . Тогда
по теореме о трёх перпендикулярах PE 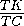 ML , значит, AEP —
линейный угол двугранного угла между секущей плоскостью и плоскостью
основания пирамиды, т.е.
ML , значит, AEP —
линейный угол двугранного угла между секущей плоскостью и плоскостью
основания пирамиды, т.е. 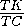 AEP=α . Кроме того, перпендикуляры TH и AF , опущенные из точек T и A на прямую PE , — перпендикуляры
к секущей плоскости. Из подобия треугольников PHT и PFA находим,
что AF=TH·
AEP=α . Кроме того, перпендикуляры TH и AF , опущенные из точек T и A на прямую PE , — перпендикуляры
к секущей плоскости. Из подобия треугольников PHT и PFA находим,
что AF=TH· 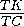 =
=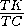 · 3=
· 3=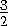 .
По теореме косинусов
.
По теореме косинусов
ML=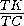 =
=
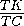 =
=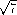 ,
,
SΔ AML= 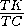 ·
· 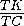 SΔ ABC=
SΔ ABC=
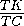 · 4
· 4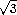 =
=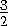
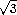 ,
,
AE = 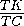 =
=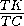 .
.
Из прямоугольного треугольника AFE находим, что
sin α = 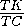 =
=
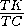 =
=
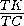 ,
,
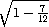 =
=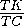 .
Следовательно,
.
Следовательно,
S=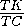 =
= 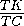 =
=
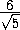 .
.
Ответ
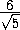 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь