Олимпиадная задача по стереометрии: точка O и сфера в параллелепипеде, 10–11 класс
Задача
Точка O расположена в сечении ACC'A' прямоугольного параллелепипеда ABCDA'B'C'D' размером2× 3× 6так, что 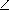 OCB +
OCB + 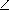 OCD +
OCD + 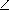 OCC' = 180o .
Сфера с центром в точке O касается плоскостей A'B'C' , CC'D и не
имеет общих точек с плоскостью BB'C . Найдите расстояние от точки O до этой плоскости.
OCC' = 180o .
Сфера с центром в точке O касается плоскостей A'B'C' , CC'D и не
имеет общих точек с плоскостью BB'C . Найдите расстояние от точки O до этой плоскости.
Решение
Обозначим 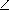 OCB =α ,
OCB =α , 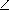 OCD=β ,
OCD=β , 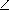 OCC'= γ .
По условию задачи α+β+γ=180o .
Отложим на луче CO отрезок CE=1. Тогда проекции точки E на прямые CB , CD и CC' равны cos α , cos β и cos γ соответственно. По теореме о квадрате диагонали
прямоугольного параллелепипеда cos2 α+ cos2 β+
cos2 γ=1, а т.к. γ = 180o-α-β , то
OCC'= γ .
По условию задачи α+β+γ=180o .
Отложим на луче CO отрезок CE=1. Тогда проекции точки E на прямые CB , CD и CC' равны cos α , cos β и cos γ соответственно. По теореме о квадрате диагонали
прямоугольного параллелепипеда cos2 α+ cos2 β+
cos2 γ=1, а т.к. γ = 180o-α-β , то
cos2 α+ cos2 β+ cos2(180o-α-β)=1, cos2 α+ cos2 β+ cos2(α+β)=1,
cos 2α + cos 2β +2 cos2(α+β)=0, 2 cos (α+β) cos (α -β)+2 cos2(α+β)=0,
cos (α+β)( cos (α-β)+ cos (α+β))=0, cos (α+β) cos α cos β=0, cos γ cos α cos β = 0.
CH=CD· 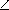 = 6·
= 6· 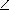 =4.
=4.
Ответ
Чтобы оставлять комментарии, войдите или зарегистрируйтесь