Олимпиадная задача по планиметрии: точка с заданными отношениями площадей в четырёхугольнике
Задача
В четырёхугольнике ABCD найдите такую точку E , для которой отношение площадей треугольников EAB и ECD было равно 1:2, а треугольников EAD и EBC — 3:4, если известны координаты всех его вершин: A(-2;-4), B(-2;3), C(4;6), D(4;-1).
Решение
Поскольку
= 
=
,
= 
=
= ,
=
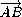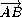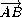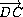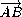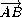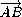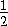равносильно тому,
что их общая вершина E лежит на прямой, параллельной основаниям и отстоящей
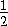от них на расстояния, отношение которых равно , т.е. на
оси ординат.
Пусть прямая BC пересекает ось ординат в точке P , а прямая AD —
в точке Q . Если O — начало координат, то OP=3и OQ = 4.
У треугольников EAD и EBC равные и
параллельные основания AD и BC , поэтому равенство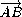 
=
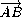равносильно тому,
что их общая вершина E лежит на прямой, параллельной основаниям и отстоящей
от них на расстояния, отношение которых равно =
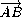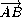, т.е.
на прямой, проходящей через точку O .
Следовательно, точка E — начало координат.
Ответ
E(0;0).
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет