Олимпиадная задача по планиметрии: углы треугольника OHC, 8-9 класс
Задача
В треугольнике ABC известно, что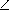 
B = 50o , 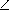C = 70o . Найдите углы треугольника OHC , где H — точка пересечения высот, O — центр окружности,
вписанной в треугольник ABC .
Решение
Заметим, что
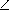CHB = 180o- 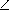BAC =
180o-60o = 120o.
Пусть CC1и BB1— высоты треугольника ABC . Из прямоугольных треугольников CC1B и BB1C находим, что
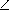BCH = 90o- 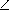ABC =
90o-50o = 40o,
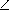CBH = 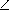CBB1=90o-70o=20o,
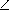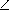OCH = BCH - 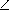BCO =
40o- 35o = 5o.
Лучи CO и BO — биссектрисы углов ACB и ABC , поэтому
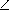COB = 90o+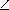
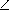BAC =
90o+30o = 120o.
Из точек H и O , лежащих по одну сторону от прямой BC , отрезок BC виден под одним и тем же углом (120o ), значит, точки B , O , H и C лежат на одной окружности. Следовательно,
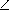COH = 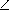CBH = 90o- 70o= 20o,
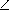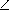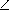CHO = 180o - OCH - COH =
180o-5o-20o=155o.
Ответ
20o ,5o ,155o .
Чтобы оставлять комментарии, войдите или зарегистрируйтесь