Олимпиадная задача по планиметрии: точки на окружности и касательной, сложность 3 из 5
Задача
Точки A , B и C лежат на окружности радиуса 2
с центром O , а точка K — на прямой, касающейся
этой окружности в точке B , причём 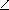 AKC =
46o , а длины отрезков AK , BK и CK образуют
возрастающую геометрическую прогрессию (в указанном
порядке). Найдите угол AKO и расстояние между точками A и C . Какой из углов больше: ACK или AOK ?
AKC =
46o , а длины отрезков AK , BK и CK образуют
возрастающую геометрическую прогрессию (в указанном
порядке). Найдите угол AKO и расстояние между точками A и C . Какой из углов больше: ACK или AOK ?
Решение
Из неравенства AK<BK<CK следует, что отрезок CK пересекает окружность в некоторой точке N , а продолжение отрезка AK пересекает окружность в некоторой точке M . Обозначим AK=x , BK=y , CK=z . Числа x , y и z в указанном порядке образуют геометричекую прогрессию, поэтому y2=xz . С другой стороны, по теореме о касательной и секущей y2=BK2=x· KM = z· KN , поэтому x· KM=xz и z· KN =xz , откуда находим KM=z=KC и KN =x=KA . Треугольники KOM и KOC равны по трём сторонам, поэтому KO — биссектриса угла CKA , следовательно,
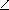 AKO=
AKO= 
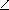 AKC = 23o.
AKC = 23o.
Из равнобедренного треугольника KCM находим, что
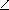 AMC = 90o-
AMC = 90o-
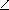 AKC =
90o-23o= 67o.
AKC =
90o-23o= 67o.
AC=2R sin 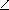 AMC = 2· 2 sin 67o=4 sin 67o.
AMC = 2· 2 sin 67o=4 sin 67o.
В четырёхугольнике AOCK известно, что
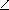 AOC +
AOC + 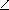 AKC = 2·
AKC = 2· 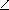 AMC +
AMC + 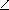 AKC=
2· 67o+46o=180o,
AKC=
2· 67o+46o=180o,
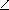 ACK =
ACK = 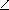 AOK .
AOK .
Ответ
23o ,4 sin 67o ; одинаковы.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь