Олимпиадная задача: биссектриса и окружность в треугольнике KLM, планиметрия
Задача
Отрезок KB является биссектрисой треугольника KLM .
Окружность радиуса 5 проходит через вершину K ,
касается стороны LM в точке B и пересекает сторону KL в точке A . Найдите угол MKL и площадь
треугольника KLM , если ML=9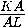 , KA:LB=5:6.
, KA:LB=5:6.
Решение
Пусть окружность пересекает сторону KM в точке C . Из теоремы об угле между касательной и хордой следует, что
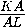 ABL =
ABL = 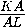 AKB =
AKB = 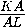 BKC =
BKC = 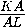 BAC,
BAC,
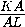 =
=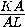 =
=
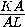 =
=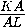 ,
AC=
,
AC=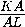 · ML=
· ML=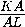 · 9
· 9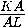 =5
=5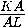 .
.
sin 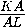 AKC =
AKC = 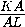 =
=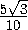 =
=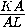 ,
,
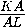 MKL =
MKL = 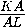 AKC = 60o или
AKC = 60o или 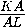 MKL=
MKL=
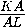 AKC = 120o .
Второй случай невозможен, т.к. тогда градусная мера дуги ABC равна240o , и поэтому расстояние от точки K до прямой AC меньше
расстояния от точки B до этой прямой. В то же время, отношение
этих расстояний равно
AKC = 120o .
Второй случай невозможен, т.к. тогда градусная мера дуги ABC равна240o , и поэтому расстояние от точки K до прямой AC меньше
расстояния от точки B до этой прямой. В то же время, отношение
этих расстояний равно 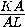 =
=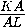 .
Следовательно,
.
Следовательно, 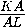 MKL = 60o .
Положим KC=5b , CM=4b . По теореме о касательной и секущей
MKL = 60o .
Положим KC=5b , CM=4b . По теореме о касательной и секущей
BM = 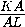 =
=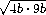 =6b,
=6b,
ML2=KM2+KL2-2KM· KL cos 60o, (6a+6b)2=81b2+81a2-81ab,
a+b=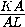 ML=
ML=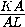 · 9
· 9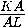 =
=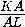
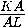 ,
,
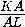
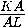 )2=
)2=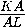 ,
ab=
,
ab=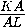 .
.
SΔ KLM=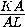 · 9a· 9b· sin 60o=
· 9a· 9b· sin 60o=
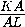 =
=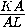 =
=
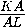 .
.
Ответ
60o , 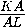 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет