Олимпиадная задача по планиметрии: прямая Гаусса для четырёхугольника
Задача
Продолжения противоположных сторон AB и CD четырёхугольника ABCD пересекаются в точке P , а продолжения сторон BC и AD — в точке Q . Докажите, что середины диагоналей AC и BD , а также середина отрезка PQ лежат на одной прямой (прямая Гаусса}.
Решение
Пусть K , L и M — середины AC , BD и PQ соответственно, а точки P1, A1и D1— середины сторон соответственно AD , DP и AP треугольника APD . Тогда точки D1, K и P1— лежат на одной прямой — средней линии треугольника APD . Аналогично, точки A1, L , P1лежат на одной прямой и точки D1, M , A1лежат на одной прямой. Применив теорему Менелая к треугольнику APD и прямой BQ , получим, что
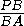 ·
· 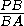 ·
· 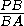 =1,
=1,
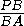 =
=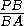 ,
,
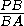 =
=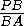 ,
,
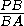 =
=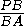 ,
,
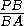 ·
· 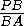 ·
· 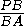 =
=
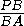 ·
· 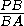 ·
· 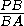 =1.
=1.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет