Олимпиадная задача по планиметрии: площадь восьмиугольника в параллелограмме
Задача
Середина каждой стороны параллелограмма соединена с концами противоположной стороны. Найдите площадь восьмиугольника, образованного пересечениями проведённых отрезков, если площадь параллелограмма равна 1.
Решение
Пусть K , L , M и N — середины сторон соответственно AB , BC , CD и AD параллелограмма ABCD площади 1, O — центр
параллелограмма. Тогда площадь параллелограмма KBLO равна 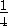 , а площадь треугольника KLO равна
, а площадь треугольника KLO равна 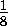 .
Пусть прямые AL и BN пересекаются в точке P , прямые BM и CK — в точке Q , а прямые AL и CK — в точке H .
Тогда P , H и Q — три последовательные вершины восьмиугольника,
о котором говорится в условии задачи. При этом P — середина стороны KO треугольника KLO , Q — середина стороны LO , а H —
точка пересечения медиан LP и KQ этого треугольника, поэтому
площадь четырёхугольника OPHQ равна трети площади треугольника KLO , т.е.
.
Пусть прямые AL и BN пересекаются в точке P , прямые BM и CK — в точке Q , а прямые AL и CK — в точке H .
Тогда P , H и Q — три последовательные вершины восьмиугольника,
о котором говорится в условии задачи. При этом P — середина стороны KO треугольника KLO , Q — середина стороны LO , а H —
точка пересечения медиан LP и KQ этого треугольника, поэтому
площадь четырёхугольника OPHQ равна трети площади треугольника KLO , т.е. 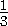 ·
· 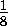 =
= 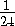 .
Осталось заметить, что площадь восьмиугольника в четыре раза больше
площади четырёхугольника OPHQ , а значит, равна4·
.
Осталось заметить, что площадь восьмиугольника в четыре раза больше
площади четырёхугольника OPHQ , а значит, равна4· 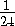 =
=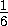 .
.
Ответ
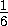 .
.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь