Олимпиадная задача по планиметрии: площадь треугольника при сторонах больше 100
Задача
Каждая сторона треугольника больше 100. Может ли его площадь быть меньше 0,01?
Решение
Рассмотрим равнобедренный треугольник ABC с основанием BC=200и высотой AM<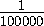 . Высота AM этого треугольника является медианой, поэтому BM=CM = 100, а т.к. AC=BC>BM=100, то все стороны
треугольника больше 100. В то же время,
. Высота AM этого треугольника является медианой, поэтому BM=CM = 100, а т.к. AC=BC>BM=100, то все стороны
треугольника больше 100. В то же время,
SΔ ABC = 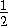 BC· AM =100· AM <
100·
BC· AM =100· AM <
100· 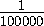 =
= <0,01.
<0,01.
Ответ
Может.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет