Олимпиадная задача по планиметрии и стереометрии для 9–11 классов от Ивлева Ф.: касание окружностей с дугами α и β

Решение 1:   Пусть O – точка пересечения прямых AB и CD, Ω₁ и Ω₂ – окружности, симметричные ω₁ и ω₂ относительно биссектрисы угла AOD. Рассмотрим окружности Ω₄ и Ω₃, полученные из Ω₁ и Ω₂ инверсией относительно окружности с центром O и радиусом 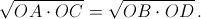    Они, очевидно, касаются. При этом Ω₄ проходит через точки C и D и может быть получена из Ω₁ не только инверсией, но и гомотетией с центром O и коэффициентом  OD : OA = OC : OB.  Поэтому градусная мера дуги CD в Ω₄ равна α. Следовательно, Ω₄ совпадает с ω₄. Аналогично Ω₃ совпадает с ω₃.

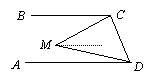
Решение 2:   Лемма. Пусть точка M лежит между основаниями BC и AD трапеции ABCD по ту же сторону от CD, что и точка A. Тогда  ∠CMD = ∠BCM + ∠ADM.

  Доказательство очевидно из левого рисунка.

  Обозначим черезPточку касания окружностей ω₁и ω₂, а черезQ– вторую точку пересечения описанных окружностей треугольниковBCPиADP(рис. справа).  ∠APB= ∠APQ+ ∠BPQ= ∠ADQ+ ∠BCQ= ∠CQD  (по лемме). Следовательно, точкаQлежит на ω₄. Аналогично доказывается, что она лежит и на ω₃.   Углы между хордамиBPиCPи общей касательной к ω₁и ω₂равны соответственно угламBAPиCDP. Поэтому  ∠BAP+ ∠CDP= ∠BPC.  Отсюда ∠BAQ+ ∠CDQ= ∠BAD+ ∠CDA– (∠QAD+ ∠QDA) = ∠BAD+ ∠CDA+ ∠AQD– 180° = ∠BAD+ ∠CDA+ ∠APD– 180° = = ∠BAP+ ∠CDP= ∠BPC= ∠BQC.   Следовательно, через точкуQможно провести прямую, составляющую сBQиCQуглы, соответственно равные угламBAQиCDQ. Она и будетобщейкасательной к ω₃и ω₄в точкеQ.   Замечание. Детали доказательства, разумеется, зависят от взаимного расположения прямых и окружностей. Разбор остальных случаев предоставляется читателю.

Ответ задачи отсутствует