Олимпиадная задача по математике: доказательство о рёбрах параллелепипеда, 10-11 класс
Задача
В пространстве с декартовой системой координат дан прямоугольный параллелепипед, вершины которого имеют целочисленные координаты. Его объём равен 2011. Докажите, что рёбра параллелепипеда параллельны координатным осям.
Решение
По теореме Пифагора длины рёбер равны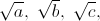 
где числа a ≤ b ≤ c – натуральны. Тогда квадрат объёма 2011² = abc.
Поскольку 2011 – простое число, то a = 1. Для b и c возможны два случая: b = 1, c = 2011 или b = c =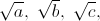 
. Ребро длины 1 идёт, очевидно, по линии сетки. В случае a = b = 1 ребро c перпендикулярно двум линиям сетки и поэтому тоже идёт по сетке. В случае b = c ребра b и c лежат в плоскости, перпендикулярной линии сетки. Но тогда 2011 должно представляться как сумма двух квадратов. Однако 2011 ≡ 3 (mod 4), а для суммы двух квадратов такое невозможно.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь