Олимпиадная задача: четыре перпендикуляра в выпуклом пятиугольнике, планиметрия

Пересечение перпендикуляров в пятиугольнике — олимпиадная задача из планиметрии

Задача

Четыре перпендикуляра, опущенные из вершин выпуклого пятиугольника на противоположные стороны, пересекаются в одной точке.

Докажите, что пятый такой перпендикуляр тоже проходит через эту точку.

Решение

Пусть O – точка пересечения перпендикуляров, опущенных из вершин A, B, C и D пятиугольника ABCDE на противолежащие стороны. Нетрудно убедиться, что точка O не может совпадать с вершиной пятиугольника. Пусть OA ⊥ CD. Тогда 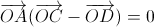, то есть 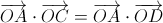. Аналогично из OB ⊥ DE, OC ⊥ EA, OD ⊥ AB получаем равенства 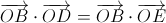, , 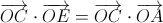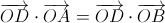. Но тогда и 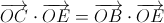, то есть 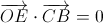. Значит, OE ⊥ BC.