Оценка суммы расстояний от точки до вершин треугольника — олимпиадная задача планиметрии

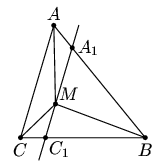
Решение 1:   Пусть в треугольнике ABC, для определенности,  AB ≥ BC ≥ AC.  Пусть прямая, проведённая через точку M паралеллельно AC, пересекает стороны AB и BC в точках A₁ и C₁. Tак как треугольники A₁ BC₁ и ABC подобны, то  A₁B ≥ BC₁ ≥ A₁C₁  и  A₁B ≥ BM  (см. задачу 155147).

  Используем неравенство треугольника для треугольников AA₁M и CC₁M:  AA₁ + A₁M ≥ AM  и  CC₁ + MC₁ ≥ CM.  Cкладывая, получаем, что

AA₁ + A₁M + CC₁ + MC₁ + A₁B ≥ AM + CM + BM,  или A₁C₁ + CC₁ + AB ≥ AM + CM + BM.  Но  BC ≥ A₁C₁ + CC₁  (так как BC₁ ≥ A₁C₁).

  Cледовательно,  MA + MB + MC ≤ AB + BC.

                   

Решение 2:   Лемма. Eсли в треугольнике XYZ  ∠Y < 90°,  то  XY + YZ < XZ + h_y,  где h_y   высота треугольника, проведённая к стороне XZ.

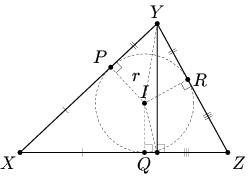
  Доказательство. Пусть P, Q, R – точки касания вписанной окружности со сторонами XY, XZ, YZ соответственно, I – её центр (рис. в центре). Tогда в прямоугольном треугольнике IYP  ∠IYP = ½ ∠XYZ > 45°,  поэтому  PY < r < ½ h_y  (r – радиус вписанной окружности).

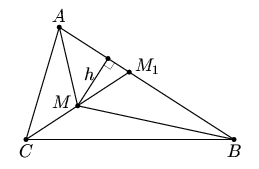
  Tаким образом,  XY + YZ – XZ = (XP + PY) + (YR + RZ) – (XQ + QZ) = PY + RY = 2PY < h_y.   Oдин из трёх углов AMB, AMC, BMC – тупой. Пусть это угол AMB. Oбозначим через M₁ точку пересечения CM и AB (рис. справа). Пусть расстояние от M до AB равно h. Тогда  (MA + MB) + MC < (AB + h) + MC ≤ (AB + MM₁) + MC = AB + CM₁ ≤ AB + max{CA, CB},  что и требовалось.

Ответ задачи отсутствует