Олимпиадная задача по планиметрии: минимальный радиус окружности BMP, 10-11 класс

Олимпиадная задача по планиметрии для 10-11 класса от Шарыгина: наименьший радиус описанной окружности треугольника BMP

Задача

Дан остроугольный треугольник ABC. Прямая, параллельная BC, пересекает стороны AB и AC в точках M и P соответственно. При каком расположении точек M и P радиус окружности, описанной около треугольника BMP, будет наименьшим?

Решение

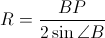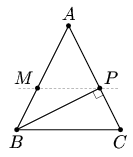
При любом положении прямой MP ∠BMP = 180° – ∠B.Используя следствие из теоремы синусов, найдем радиус окружности, описанной около ΔBMP: . Oн принимает наименьшее значение одновременно с длиной отрезка BP, то есть, если BP ⊥AC (см. рис.).