Олимпиадная задача по планиметрии о треугольнике ABC и центрe вписанной окружности

Решение 1:   Утверждение задачи означает, что C₃ – точка касания стороны AB с окружностью, вписанной в ABC (рис. слева). Так как треугольники ABC и A₁B₁C гомотетичны, то утверждение задачи равносильно тому, что C₂ – точка касания A₁B₁ и окружности, вписанной в треугольник A₁B₁C, то есть 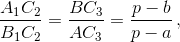    где a, b, c – стороны треугольника ABC, а p – его полупериметр.

  Так как треугольникA₁B₁C₁подобен треугольникуABCс коэффициентом ½, то высотаB₁HтреугольникаA₁B₁C₁(а, следовательно, и расстояние между прямымиA₁C₁иAC) в два раза меньше высотыh_bтреугольникаABC(рис. справа). Cледовательно, расстояние от точкиIдо прямойA₁C₁равно ½h_b – r.  Аналогично расстояние от точкиIдо прямойB₁C₁равно  ½h_a – r.   Cледовательно,  

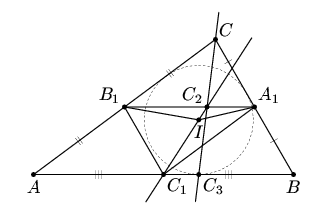
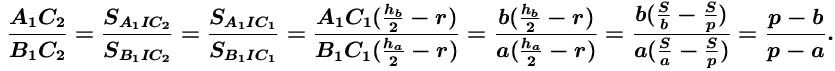
Решение 2:   Пусть T и T' – точки касания вписанной ω и вневписанной ω' окружностей со стороной AB, K – точка вписанной окружности, диаметрально противоположная T (см. рис.). При гомотетии с центром C, переводящей ω в ω', K переходит в T', поэтому C, K и T' лежат на одной прямой.

  Как известно,  AT' = BT  (см. задачу155404). ПоэтомуC₁T = C₁T'  и в треугольникеKT'TотрезокC₁Iявляется средней линией. Обозначим черезMточку пересечения прямойC₁Iс высотой треугольникаABC, опущенной из точкиC. ТогдаCKIM– параллелограмм, поэтому  CM = KI = IT.  Значит,IиMравноудалены от средней линииA₁B₁, то естьC₂является серединой отрезкаIM.   Cледовательно, точкиCиTсимметричны относительноC₂, то естьC, C₂иTлежат на одной прямой, поэтому точкаTсовпадает с точкойC₃, что и требовалось.

Ответ задачи отсутствует