Олимпиадная задача по планиметрии: построение точки для равностороннего треугольника
Задача
В окружность вписан треугольник ABC. Постройте такую точку P, что точки пересечения прямых AP, BP и CP с данной окружностью являются вершинами равностороннего треугольника.
Решение
Решение 1: Пусть искомая точка P построена и лежит внутри треугольника ABC (рис. слева). Тогда ∠APB = ∠A1C1B1 + ∠C = 60° + ∠C.
Таким образом, искомая точка P является пересечением геометрического места точек, из которых сторона AB видна под углом 60° + ∠C, и геометрического места точек, из которых сторона BC видна под углом 60° + ∠A (рис. справа).
Если, например, ∠A ≥ 120°, то искомая точка P лежит вне треугольника или на стороне BC. При этом способ построения точки P не изменится, но сторона BC будет видна из точки P не под углом 60╟ + ∠A, под углом 360° – ∠A.
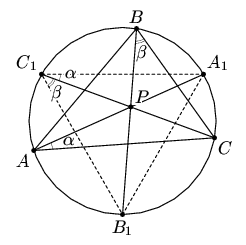
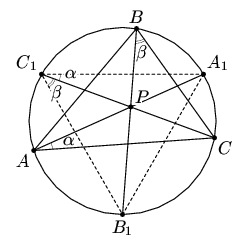
Решение 2: Из подобия треугольников APC и C1PA1 (рис. слева) следует, что AP : AC = C1P : C1A1. Аналогично BP : BC = C1P : C1B1. Cледовательно,
AP : BP = AC : BC, то есть точка P лежит на окружности Аполлония точек A и B.
Аналогично построив еще одну окружность Аполлония, например, для точек A и C, на их пересечении получим искомую точку.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь