Олимпиадная задача по планиметрии: доказательство неравенства в треугольнике
Задача
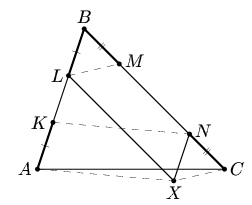
В треугольнике ABC на стороне AB выбраны точки K и L так, что AK = BL, а на стороне BC — точки M и N так, что CN = BM. Докажите, что KN + LM ≥ AC.
Решение
Первый способ. Рассмотрим для определенности конфигурацию, изображенную на рис. а. Тогда
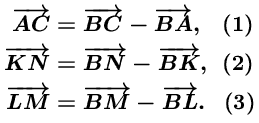
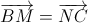 , а
, а 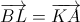 ,
то сложив равенства (2) и (3), получим, что
,
то сложив равенства (2) и (3), получим, что
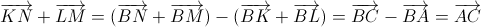 , следовательно,
, следовательно,
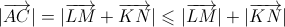 .
Заметим, что при таком решении не существенно, как расположены
точки K, L, M и N.
.
Заметим, что при таком решении не существенно, как расположены
точки K, L, M и N.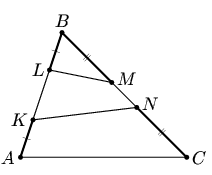 |
 |
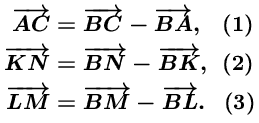 |
| Рис. а | Рис. б | Рис. в |
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет