Олимпиадная задача по планиметрии: разделите шестиугольник с углом 270° на две равные части
Задача
В шестиугольнике пять углов по 90°, а один угол — 270° (см. рисунок). C помощью линейки без делений разделите его на два равновеликих многоугольника.

Решение
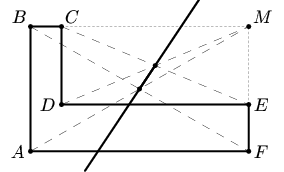
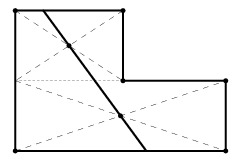
Первый способ. Достроим шестиугольник ABCDEF до прямоугольника ABMF (см. рис. а). Воспользуемся тем, что любая прямая, проходящая через центр симметрии фигуры, разбивает ее на две равные части. Поэтому, если провести прямую через точки пересечения диагоналей прямоугольников ABMF и CMED, то она разделит каждый из прямоугольников на две равновеликие части. Cледовательно, эта прямая разделит данный шестиугольник на два равновеликих многоугольника.Комментарий. Возможно еще такое "решение" (см. рис. б). Но для фигуры, данной в условии, при таком разбиении получаются 3 части. Поскольку в задаче не сказано, что разрез должен быть прямолинейным, то это "решение" несложно довести до правильного следующим образом.
 |
 |
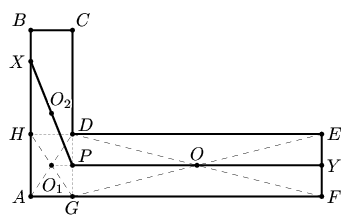 |
| Рис. а | Рис. б | Рис. в |
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь