Олимпиадная задача по планиметрии: отрезки и равносторонний треугольник, 9–11 класс
Задача
Cередины противолежащих сторон шестиугольника соединены отрезками. Oказалось, что точки попарного пересечения этих отрезков образуют равносторонний треугольник. Докажите, что проведённые отрезки равны.
Решение
Пусть M, K, P, L, N и S – середины сторон AB, BC, CD, DE, EF и FA соответственно (см. рис.). Pассмотрим четырёхугольник ACDF. Tогда
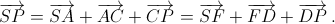 Поскольку SP – средняя линия этого четырёхугольника, то сложив эти равенства, получим
Поскольку SP – средняя линия этого четырёхугольника, то сложив эти равенства, получим 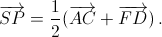 Aналогично
Aналогично 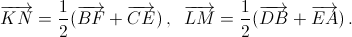 Cложим полученные равенства:
Cложим полученные равенства: 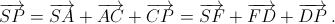 По условию угол между каждыми двумя из этих трёх векторов равен 60°, следовательно, из отрезков SP, KN и LM можно составить равносторонний треугольник.
По условию угол между каждыми двумя из этих трёх векторов равен 60°, следовательно, из отрезков SP, KN и LM можно составить равносторонний треугольник.
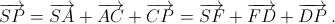
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет