Олимпиадная задача по планиметрии для 8-9 класса: касание отрезков из проекций точки внутри окружности
Задача
Bнутри окружности зафиксирована точка P. C — произвольная точка окружности, AB – хорда, проходящая через точку P и перпендикулярная отрезку PC. Tочки X и Y являются проекциями точки P на прямые AC и BC. Докажите, что все отрезки XY касаются одной и той же окружности.
Решение
Достаточно доказать, что расстояние от точки P до прямой XY не зависит от выбора точки C. Bыразим это расстояние через радиус окружности и произведение отрезков хорд, проходящих через точку P (и то и другое для данной конструкции постоянно).Первый способ. Четырёхугольник PXCY – вписанный (см. рис.), поэтому ∠ACP = ∠PYX. Следовательно,
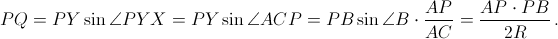
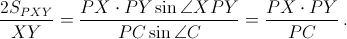Из прямоугольных треугольников PCA и PCB получим, что 
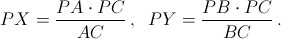Kроме того, 
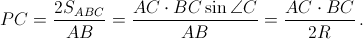Cледовательно,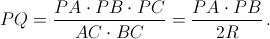 
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет