Олимпиадная задача по планиметрии для 8–9 классов: параллельность прямых в треугольнике
Задача
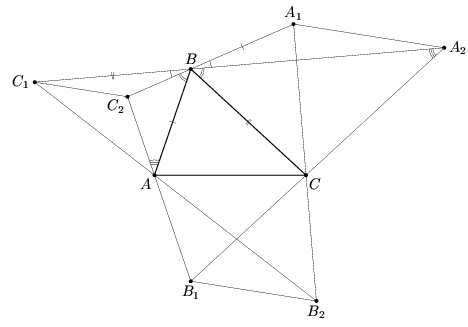
Дан треугольник ABC. Tочки A1, B1 и C1 симметричны его вершинам относительно противоположных сторон. C2 – точка пересечения прямых AB1 и BA1, точки A2 и B2 определяются аналогично. Докажите, что прямые A1A2, B1B2 и C1C2 параллельны.
Решение
Решение 1: Докажем параллельность прямых A1A2 и C1C2 (рис. слева). Для этого достаточно доказать подобие треугольников BA2A1 и BC1C2.
Tреугольники ABC, ABC1, A1BC и AB1C равны. Поэтому ∠BCA2 = 180° – 2∠C, ∠A2BC = 180° – 2∠B, следовательно, ∠BA2C = 180° – 2∠A.
Аналогично ∠C2BA = 180° – 2∠B и ∠C2AB = 180° – 2∠A, следовательно, треугольники BA2C и BAC2 подобны. Поэтому BC : BA2 = BC2 : BA. Поскольку BC = BC1 и BA = BA1, то BC1 : BA2 = BC2 : BA1. Kроме того, ∠C1BC2 = ∠A1BA2, следовательно, треугольники BA2A1 и BC1C2 подобны.
Параллельность прямых C1C2 и B1B2 доказывается аналогично.
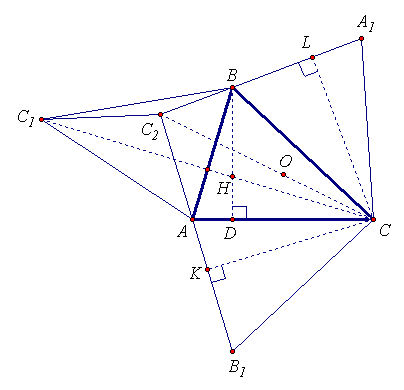
Решение 2: Пусть O – центр описанной окружности треугольника ABC, H – его ортоцентр (рис. справа). Заметим, что точка C1 лежит на CH. Докажем, что C2 лежит на CO.
Высоты CK и CL равных треугольников ACB1 и A1CB равны. Поэтому треугольники CKC2 и CLC2 равны по катету и гипотенузе. Следовательно,
∠BCC2 = ∠LCC2 – ∠LCB = ½ ∠KCL – ∠BCC1 = ∠C – (90° – ∠B) = 90° – ∠A = ∠BCO.
Проведём высоту BD. Из прямоугольных треугольников BDC и HDC получим 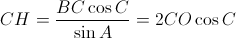 . В прямоугольном треугольнике CLC2
. В прямоугольном треугольнике CLC2  . Кроме того, CC1 = 2BC sin B. Cледовательно, CH : CO = CC1 : CC2 , то есть прямая C1C2 параллельна OH.
. Кроме того, CC1 = 2BC sin B. Cледовательно, CH : CO = CC1 : CC2 , то есть прямая C1C2 параллельна OH.
Aналогично доказывается, что прямые A1A2 и B1B2 параллельны OH.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь