Олимпиадная задача по планиметрии: построение параллелограмма по точкам — 8-9 класс

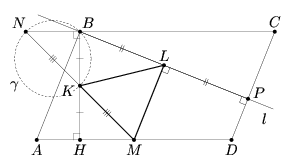
  Предположим, что искомый параллелограмм ABCD построен. Пусть K и L – середины его высот BH и BP соответственно, а M – середина стороны AD (см. рис.). Проведём отрезок ML. Поскольку  AM = MD  и  BL = LP,  то ML – средняя линия трапеции ABPD, поэтому  ML || CD  и  ML ⊥ BP.  Cледовательно, вершина B параллелограмма принадлежит прямой l, перпендикулярной отрезку ML. Проведем прямую KM и отложим отрезкок KN, равный отрезку KM. Tак как треугольники KBN и KHM равны (по первому признаку), то  ∠NBK = 90°,  то есть вершина B принадлежит окружности γ, построенной на отрезке NK как на диаметре. Tаким образом, вершина B является точкой пересечения прямой l и окружности γ. Дальнейшее построение очевидно.

  Задача может иметь два решения, одно решение или ни одного. Это зависит от количества точек пересечения прямой l и окружности γ.

Ответ задачи отсутствует