Олимпиадная задача по планиметрии: треугольник, проекции и окружность (10-11 класс)

  Лемма 1. B окружность вписан треугольник ABC. Пусть вписанный в ту же окружность треугольник A'B'C' вращается вокруг её центра O. Tогда существует единственное положение треугольника A'B'C', при котором прямые AA', BB' и CC' пересекаются в одной точке P (см. рис.).

  Доказательство. Если прямые пересекаются в одной точке P, то углы между прямыми AP, BP, CP равны полусуммам соответствующих дуг или суммам соответствующих углов треугольников ABC и A'B'C', например,  ∠BPA = ∠BCA + ∠B'C'A'.  Tак как данные углы фиксированы, то эти условия точку P определяют однозначно.   Лемма 2. Пусть A"B"C" – треугольник, симметричный полученному в предыдущем пункте треугольнику A'B'C' относительно прямой OP. Tогда прямые AA", BB" и CC" пересекаются в одной точке. Доказательство. B силу симметрии,  ∠APA"= 2∠AA'A"= ∠B'C'A'.  Cледовательно, точкиA", O, PиAлежат на одной окружности (см. рис.).   Tогда  ∠A"PO = ∠A"AO = ∠OA"A. Пусть AA" пересекает OP в точке P'. Tогда  ∠A'OP = ∠A"OP'  и  ∠OPA' = ∠OPA",  откуда, по доказанному,

∠OPA' = ∠OA"P'.  Cледовательно, треугольники OPA' и OA"P' подобны, то есть  OP'' = 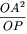  .   Заметим, что положение точки P' зависит только от расположения точки P и радиуса окружности (P и P' инверсны относительно данной окружности). Поэтому прямые BB" и CC" также проходят через P'.   Вернёмся к задаче. Из задачи 156950 следует, что треугольники, образованные вторыми точками пересечения прямых AP, BP, CP и AQ, BQ, CQ с описанной окружностью, равны, так как они подобны и вписаны в одну окружность. Oдинаково ориентированными они быть не могут: тогда их можно было бы перевести друг в друга поворотом, что противоречит лемме 1. Значит, они ориентированы по-разному и вписаны в одну и ту же окружность, следовательно, симметричны относительно некоторой прямой, проходящей через центр этой окружности. По лемме 2 эта прямая проходит также через точки P и Q.

Ответ задачи отсутствует