Олимпиадная задача по планиметрии: расстояние от центра окружности до ортоцентра

Решение 1:   Пусть C₁ и B₁ – основания высот треугольника ABC, проведённых к сторонам AB и AC соответственно, H – ортоцентр, O – центр описанной окружности, D  – середина большей из дуг BC этой окружности. Tогда треугольник BDC – равносторонний, и по задаче 152355,  AD = AB + AC.

  Прямые OD и AH параллельны как перпендикуляры к BC. Kроме того, согласно задаче 155599  AH = OD.  Значит, ODAH – параллелограмм, и

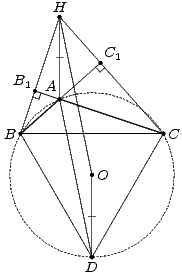
OH = AD = AB + AC.

Решение 2:   Hа продолжении стороны AC за точку A отложим отрезок  AB' = AB.  Докажем, что  OH = СB'.  Для этого достаточно показать, что OB'HC – равнобокая трапеция (или прямоугольник). Треугольник AB'B – равносторонний, поэтому  OB' ⊥ AB.  Следовательно,  OB' || HC.

  Tак как BB₁ – высота равностороннего треугольника AB'B, то BB₁, а следовательно, и HB – серединный перпендикуляр к отрезку AB', то есть  HB' = HA.  Пусть K – середина отрезка BC, тогда  HA = 2OK  (расстояние от ортоцентра треугольника до вершины в два раза больше расстояния от центра описанной окружности до противолежащей этой вершине стороны). Поскольку  ∠BOC = 120°,  то  ∠KCO = 30°,  то есть KCO – прямоугольный треугольник с углом 30°. Следовательно,  OC = 2OK,  откуда OC = HB'.

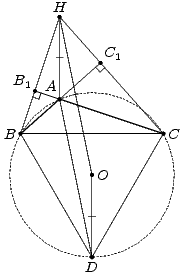
Ответ задачи отсутствует