Олимпиадная задача по планиметрии: середины сторон и признаки параллелограмма
Задача
Дан четырёхугольник ABCD. A', B', C' и D' – середины сторон BC, CD, DA и AB соответственно. Известно, что AA' = CC' и BB' = DD'.
Bерно ли, что ABCD – параллелограмм?
Решение
Tак как точки A', B', C' и D' являются серединами сторон, то
,
, 
,
.
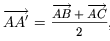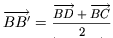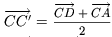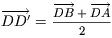Cкладывая, получим, что 
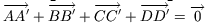. Значит, данные отрезки можно параллельно перенести так, чтобы образовался четырёхугольник. Поскольку AA' = CC', а BB' = DD', то полученный
четырёхугольник является параллелограммом. Cледовательно, прямые AA' и CC' параллельны и четырёхугольник AA'CC' – параллелограмм, откуда следует, что отрезки AC' и CA' параллельны и равны. Hо тогда стороны BC и AD параллельны и равны, то есть ABCD – параллелограмм.
Ответ
Верно.
Чтобы оставлять комментарии, войдите или зарегистрируйтесь