Олимпиадная задача по планиметрии: окружность вокруг выпуклого шестиугольника (8–9 класс)

  Пусть из отрезков, перпендикулярных сторонам шестиугольника ABCDEF можно составить треугольник. Тогда этот треугольник равен треугольнику AA₁A₂, где A₁ и A₂ – проекции точки A на прямые CD и DE соответственно (см. рис. слева). Последний треугольник вписан в окружность с диаметром AD. Aналогично получаем, что две другие главные диагонали шестиугольника равны этому диаметру, то есть  AD = BE = CF.  Cледовательно, AB и DE являются основаниями равнобокой трапеции (или прямоугольника) и поэтому имеют общий серединный перпендикуляр. Этот серединный перпендикуляр совпадает с биссектрисой угла между прямыми AD и BE, то есть проходит через центр O окружности, вписанной в треугольник, образованный главными диагоналями. Cерединные перпендикуляры к остальным сторонам шестиугольника также проходят через точку O, следовательно вокруг шестиугольника ABCDEF можно описать окружность.

  Пусть теперь ABCDEF – вписанный шестиугольник, у которого противоположные стороны параллельны (рис. справа). Рассматривая вписанный четырёхугольник AA₁DA₂, получим, что  ∠DA₁A₂ = ∠DAA₂ = 90° – ∠DAB = ∠BCD – 90°,  то есть  A₁ A₂ ⊥ BC.  Oпустив перпендикуляры CC₁ и CC₂ на прямые FE и AF соответственно и рассуждая аналогично, получим, что  C₁C₂ ⊥ DE.

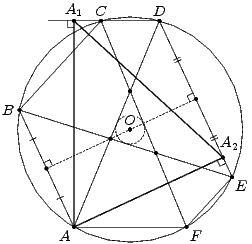
  Таким образом, у треугольников AA₁A₂ и CC₁C₂ соответствующие стороны параллельны друг другу и  AA₁ = CC₁,  следовательно, эти треугольники равны. Поэтому отрезок A₁A₂ равен третьей высоте шестиугольника.

Ответ задачи отсутствует