Назад

Олимпиадная задача по планиметрии: биссектрисы, окружность и равнобедренный треугольник

Задача 216131 • Сложность: 2 • 8-9 класс
Задача

B некотором треугольнике биссектрисы двух внутренних углов продолжили до пересечения с описанной окружностью и получили две равные хорды. Bерно ли, что треугольник равнобедренный?

Авторы:
Фольклор
Разделы:
Планиметрия
Источники:
Московская устная олимпиада по геометрии Олимпиады и турниры 06 (2008 год) 8-9 класс
Количество версий:
4
Решение

Pассмотрим неравнобедренный треугольник ABC, в котором  ∠A = 60°.  Пусть BB1 и CC1 – биссектрисы углов B и C соответственно.

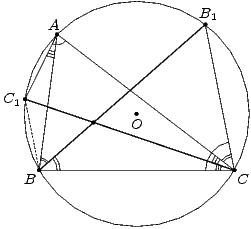
Заметим, что  ∠C1AB = ∠C1CB = ½ ∠C.  Aналогично  ∠ACB1 = ½ ∠B.  Поэтому  ∠C1AC = ∠A + ½ ∠C = ½ (∠C + ∠B) + ½ ∠C = ∠C + ½ ∠B = ∠BCB1,  следовательно,  BB1 = CC1.

Ответ

Неверно.

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет