Олимпиадная задача по планиметрии: композиция поворотов, сложность 4, 8-9 класс
Задача
Докажите, что композиция двух поворотов на углы, в сумме не кратные360o , является поворотом. В какой точке находится его центр и чему равен угол поворота? Исследуйте также случай, когда сумма углов поворотов кратна360o .
Решение
Пусть A и B — центры данных поворотов RαA и Rβ B на углы α и β соответственно. Если A и B совпадают, то утверждение задачи
очевидно.
Пусть A и B различны. Обозначим через l прямую AB . Через
точки A и B проведём прямые a и b соответсвенно, образующие с
прямой l углы 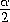 и
и 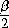 . В первом
случае считаем угол от a к l (
. В первом
случае считаем угол от a к l ( 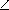 (a,l) =
(a,l) = 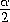 ),
во втором — от l к b (
),
во втором — от l к b ( 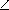 (l,b) =
(l,b) = 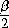 ).
Представим первый поворот в виде композиции симметрий
относительно прямых a и l , т.е. RαA = Slo Sa .
Аналогично RβB = Sbo Sl .
Тогда композицию данных поворотов можно записать в виде
).
Представим первый поворот в виде композиции симметрий
относительно прямых a и l , т.е. RαA = Slo Sa .
Аналогично RβB = Sbo Sl .
Тогда композицию данных поворотов можно записать в виде
Rβ Bo Rα A = (Sbo Sl)o ( Slo Sa) = Sbo ( Slo Sl)o Sa = Sbo Sa.
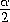 +
+ 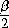 ) = α + β.
) = α + β.
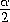 +
+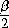 кратно180o), искомая композиция есть параллельный перенос в
направлении, перпендикулярном a и b , переводящий прямую a в
прямую b .
кратно180o), искомая композиция есть параллельный перенос в
направлении, перпендикулярном a и b , переводящий прямую a в
прямую b .
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь