Олимпиадная задача по планиметрии: минимизация суммы расстояний в треугольнике

Пусть P — некоторая точка внутри остроугольного треугольника ABC (рис.1). При повороте на60^o вокруг вершины A треугольник ABP переходит в равный ему треугольник AP1B1, а треугольник AP1P — равносторонний. Поэтому

PB + PA + PC = BP1 + P1P + PC 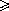B1C,

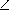причём равенство достигается только в случае, когда точки P1и P лежат на отрезке B1C . Тогда APC = 120^o , т.е. сторона AC видна из точки P под углом120^o . Аналогично докажем, что 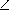APB = 120^o . Следовательно, BPC = 120^o (рис.2). Таким образом, каждая сторона треугольника видна из искомой точки P под углом120^o . Поэтому для построения точки P достаточно построить на двух сторонах треугольника как на хордах дуги, вмещающие углы120^o .

Пусть P — точка, внутри треугольника ABC , из которой все стороны видны под углом120^o (рис.3). Через вершины A , B и C проведём прямые, перпендикулярные отрезкам PA , PB и PC . Пусть M , N и K — точки пересечения этих прямых. Тогда треугольник MNK — равносторонний. Если Q — произвольная точка внутри треугольника ABC , а X , Y и Z — её проекции на стороны KN , KM и MN треугольника MNK , проходящие через точки A , B и C соответственно, то

PA + PB + PC = QX + QY + QZ

(каждая из этих сумм равна высоте треугольника MNK ). Поскольку QX QA , QY QB и QZ 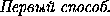QC , то

PA + PB + PC 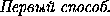QA + QB + QC.

Ответ задачи отсутствует