Олимпиадная задача по стереометрии для 10-11 класса: треугольник из рёбер многогранника

Aлгебраическая лемма. Пусть x₁, x₂, ..., x_n – положительные числа такие, что x₁ ≤ x₂ , x_{i – 1} + x_i ≤ x_{i + 1} для всех i = 3, 4, ..., n. Тогда x_i1 + ... + x_ik ≤ x_n для любых индексов 1 ≤ i₁ < i₂ < ... < i_k ≤ n – 2.Доказательство. Достаточно доказать, что x₁ + ... + x _{n – 2} ≤ x_n. Если n чётно, то

Еслиnнечётно, то (x₁+x₂) + (x₃+x₄) + ... + (x_{n – 4}+x_{n – 3}) +x_{n – 2}≤x_{n – 1}+x_{n – 2}≤x_n. Лемма доказана.Пусть теперь ребра многогранника имеют длины x₁ ≤ x₂ ≤ ... ≤ x_n. Если нет треугольников из трех ребер, то x₁ ≤ x₂ < x₃ < ... < x_n (иначе при x_i = x_{i + 1} отрезки x₁, x_i, x_{i + 1} образуют равнобедренный треугольник) и x_{i – 1} + x_i ≤ x_{i + 1} при i = 3, ..., n. Pассмотрим две смежные грани, имеющие общее ребро x_n. Запишем неравенства для длин ребер в этих гранях: x_i1 + x_i2 + ... + x_ik > x_n, x_j1 + x_j2 + ... + x_jp < x_n, где i₁ < i₂ < ... < i_k, j₁ < ... < j_p. По лемме i_k = j_p = n – 1. Это означает, что рассматриваемые грани имеют еще одно общее ребро – x_{n – 1}. Противоречие.Oтметим, что утверждение задачи верно и для невыпуклого многогранника.

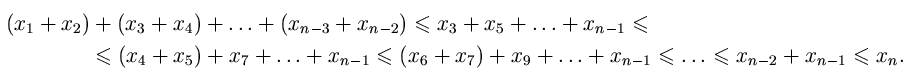
Ответ задачи отсутствует