Построение треугольника по стороне, радиусу вписанной и вневписанной окружности — олимпиадная задача планиметрии
Задача
Постройте треугольник по стороне, радиусу вписанной окружности и радиусу вневписанной окружности, касающейся этой стороны. (Исследование проводить не требуется.)
Решение
Предположим, что искомый треугольник ABC построен. Будем считать, что известна длина стороны AC и радиусы окружностей, которые её касаются.Пусть K, L и N – точки касания вписанной окружности со сторонами AC, AB и BC соответственно (см. рис. а), точки M, P и T – точки касания вневписанной окружности со прямыми AC, AB и BC соответственно.Первый способ. Докажем, что NT = AC. Действительно, из равенства отрезков касательных следует, что AK = AL , BL = BN , CK = CN , откуда AC = P – BN (P – полупериметр треугольника ABC). Кроме того, BP = BT и BP + BT = AB + AM + BC + CM, откуда BT = P. Но тогда NT = P – BN , то есть, AC = NT.
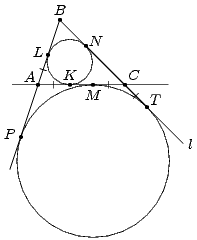 |  |
| Рис. а | Рис. б |
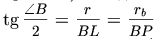 . Из доказанного выше следует, что BL = p – AC,
BP = p. То есть,
. Из доказанного выше следует, что BL = p – AC,
BP = p. То есть,
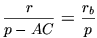 , откуда
, откуда 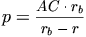 и
и 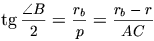 . Зная
. Зная 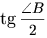 , мы можем построить угол, равный
, мы можем построить угол, равный 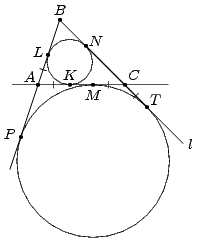 ,
а, следовательно, и угол, равный углу B.Отсюда вытекает следующий способ построения. Построим угол, равный углу B,
и впишем в него окружности с данными радиусами. Затем проведем общую внутреннюю касательную к этим
окружностям.
,
а, следовательно, и угол, равный углу B.Отсюда вытекает следующий способ построения. Построим угол, равный углу B,
и впишем в него окружности с данными радиусами. Затем проведем общую внутреннюю касательную к этим
окружностям.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь