Назад

Олимпиадная задача по планиметрии: построение ромба из параллелограмма (8-9 класс)

Задача 216078 • Сложность: 1 • 8-9 класс
Задача

На рисунке изображен параллелограмм и отмечена точка P пересечения его диагоналей. Проведите через P прямую так, чтобы она разбила параллелограмм на две части, из которых можно сложить ромб.

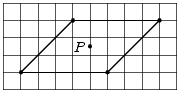
Решение

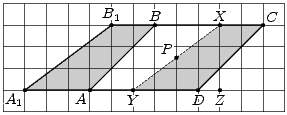
Пусть ABCD  – данный параллелограмм, P  – точка пересечения его диагоналей. Отметим на сторонах BC и AD точки X и Y так, как показано на рисунке, Z  – основание перпендикуляра, опущенного из точки X на прямую AD. Применив для треугольника XYZ теорему Пифагора, получим, что . Тогда из четырехугольников ABXY и YXCD можно сложить ромб A1B1XY.

Отметим, что такая прямая существует для любого параллелограмма. Действительно, пусть в параллелограмме ABCD AB < BC и ∠ABC  – не острый (см. рис. ниже). Тогда существует отрезок XY с концами на сторонах BC и AD, равный BC. Для того, чтобы его построить, достаточно провести окружность с радиусом, равным 1/2BC, и центром в точке P. Она пересечет отрезок BC хотя бы в одной точке, поскольку расстояние от точки P до прямой BC не больше, чем 1/2 AB, т. е. не больше, чем 1/2BC, а PC > 1/2BC.

Ответ

Ответ задачи отсутствует

Чтобы оставлять комментарии, войдите или зарегистрируйтесь

Войти Зарегистрироваться
Комментариев нет