Олимпиадная задача по планиметрии: Перпендикулярность прямых в параллелограмме
Задача
Из вершины A параллелограмма ABCD опущены высоты AM на BC и AN на CD. P – точка пересечения BN и DM. Докажите, что прямые AP и MN перпендикулярны.
Решение
Пусть высоты, проведенные из вершин M и N треугольника AMN пересекаются в
точке H и пересекают прямые AD и AB в точках K и L соответственно (см. рис.).
Тогда достаточно
доказать, что A, H и P лежат на одной прямой. Заметим, что данные высоты параллельны сторонам
параллелограмма. Для треугольника DMC и прямой BN запишем теорему Менелая:
.
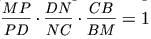Заметим, что в силу параллельности 
,
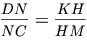а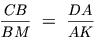 
. Тогда для
треугольника KMD и точек A, H и P выполнено условие, что 
,
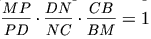то есть по теореме
Менелая, они лежат на одной прямой.Cлучай, когда угол A – острый, рассматривается аналогично.
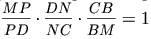
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь