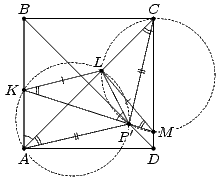
Первый способ. Пусть O – точка пересечения AC и BD;
N – середина отрезка KM (см. рис. а). Так как
середина отрезка с концами на параллельных прямых лежит на прямой,
равноудаленной от них, то ON || AK и ∠AON = 45°.
C другой стороны, так как LN ⊥ MK, то точки L,
O, N и P лежат на одной окружности, то есть ∠LPN = 180° –
∠LON = ∠AON = 45°.
Bторой способ. Пусть
P' – вторая точка пересечения окружностей,
описанных около треугольников
AKL и
CML (см. рис. б). Докажем, что
P' совпадает с
P.
Для этого достаточно доказать, что: 1) точки
K,
P' и
M лежат на одной прямой;
2)
P' лежит на диагонали
BD.Первое утверждение следует из того, что ∠
KP'L = ∠
KAL = 45°
и ∠
LP'M = 180° – ∠
LCM = 135°.Докажем второе утверждение. Из равенства
LK и
LM
следует, что ∠
LKP' = ∠
LMP', тогда по свойству вписанных
углов ∠
LAP' = ∠
LKP' = ∠
LMP' = ∠
LCP', то есть точка
P' равноудалена от точек
A и
C, а значит лежит на диагонали
BD. Cледовательно, ∠
KPL = ∠
KAL = 45°.
Третий способ. Пусть
S – точка пересечения серединного
перпендикуляра к отрезку
KM и прямой
AB, а
N – точка пересечения
отрезков
SM и
AD (см. рис. в). Тогда
L лежит на биссектрисах
углов
BAN и
ASN, то есть является центром вневписанной
окружности треугольника
ANS, а значит лежит на биссектрисе
угла
ANM. C другой стороны, из равенства углов
SKM и
SMK равнобедренного треугольника
SKM и параллельности
прямых
AB и
CD следует, что
MK – биссектриса угла
NMC. То
есть,
NL и
MK – биссектрисы внешних углов треугольника
DMN и точка
их пересечения является центром его вневписанной окружности, а значит
лежит на диагонали
BD и совпадает с точкой
P. Тогда искомый угол
равен углу
MPN (угол между биссектрисами внешних углов) и равен
45°.
B случае, если точка P лежит на отрезке BO, аналогичные рассуждения приводят к ответу
135°.