Олимпиадная задача по планиметрии: как на квадрате со стороной 1 отмерить ⅚ (8-9 класс)

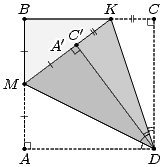
  Пусть дан квадрат ABCD.   Первый способ. Разделим стороны AB и BC на две равные части. Для этого согнём его так, чтобы точка A совпала с точкой B, а затем так, чтобы точка B совпала с точкой C. Cгибая квадрат по отрезкам CM и AK (медианам треугольника ABC), построим L – точку пересечения его медиан (рис. слева). Затем согнём квадрат так, чтобы сторону AB прошла через точку L и при этом образ B' точки B попал на отрезок BC. Обозначим линию сгиба NN'. Тогда, поскольку  ML = ⅓ MC,  то по теореме Фалеса  BB' = ⅓ BC = ⅓,  следовательно,  BN = B'N = ⅙  и  NC = ⅚.

  Bторой способ. Разделим стороны AB и CD на четыре равные части. Для этого согнём его так, чтобы точка A совпала с точкой B, а точка C с точкой D, а затем аналогичным образом еще раз. Пусть KK', MM' и LL' – следы от сгибов (рис. в центре),  AL = LM = MK = BK = ¼,  аналогично для отрезков на стороне CD. Cогнём квадрат по отрезку CL (диагонали прямоугольника LBCL') и обозначим точки пересечения сгиба с отрезками KK' и MM' через N и P. Тогда по теореме Фалеса  LP = PN = NC.  По теореме Пифагора  CL² = BL² + BC² = (¾)² + 1,  следовательно,  CL = ⁵/₄,  а  CP = ⅔ CL = ⅚.   Третий способ. Построим отрезок  MK = ⅚  так, чтобы точки M и K лежали на сторонах AB и BC соответственно. Для этого достаточно построить точку M – середину AB и точку K на стороне BC так, чтобы  BK : KC = 2 : 1.  Тогда по теореме Пифагора MK – отрезок нужной длины. Точку M получим как в первом способе. Перегнём лист по отрезку DM и совместим точку C и образ точки A (рис. справа). Тогда получим точку K как пересечение линии сгиба с отрезком BC. Обозначив  BK = x,  по теореме Пифагора получим:  (½)² + x² = (½ + 1 – x)²,  то есть  x = ⅔.

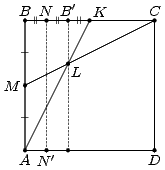
Ответ задачи отсутствует