Олимпиадная задача по планиметрии: четырёхугольник на окружности и центры треугольников

Решение 1:   Пусть R – радиус окружности, P – середина AC, Q – середина BD, O₁ и O₂ – центры описанных окружностей треугольников AOC и BOD соответственно.

  Опустим перпендикуляр O₁N на радиус OA. Из подобия треугольников AOP и O₁ON получаем  OP : OA = ON : OO₁,  то есть  OP·OO₁ = ½ R².  Аналогично

OQ·OO₂ = ½ R².  Поэтому  OP : OQ = OO₂ : OO₁,  значит, треугольники OPO₂ и OQO₁ подобны (у них общий угол при вершине O). По условию угол OQO₁ прямой, следовательно, и угол OPO₂ прямой, что и требовалось доказать.   Замечание для знатоков. Прямые AC и BD – поляры соответственно точек O₁ и O₂ относительно окружности радиуса ^R/₂ с центром O. Поэтому утверждение задачи есть переформулировка известной теоремы:     если точка X лежит на поляре точки Y, то точка Y лежит на поляре точки X.   Выше как раз приведено одно из доказательств этой теоремы.

Решение 2:   Утверждение задачи есть частный случай следующего утверждения.     Пусть центр окружности Ω₁ лежит на радикальной оси окружностей Ω₂ и Ω₃, а центр окружности Ω₂ лежит на радикальной оси окружностей Ω₁ и Ω₃. Тогда центр окружности Ω₃ лежит на радикальной оси окружностей Ω₁ и Ω₂.   (В нашем случае Ω₁, Ω₂ и Ω₃ – описанные окружности треугольников ABC, AOC и BOD соответственно.)  Доказательство сводится к тривиальной проверке следствия:

 

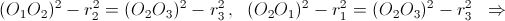
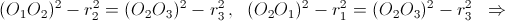
Ответ задачи отсутствует