Олимпиадная задача о встречах велосипедистов на кольцевом треке для 8–11 класса
Задача
На кольцевом треке 2n велосипедистов стартовали одновременно из одной точки и поехали с постоянными различными скоростями (в одну сторону). Если после старта два велосипедиста снова оказываются одновременно в одной точке, назовём это встречей. До полудня каждые два велосипедиста встретились хотя бы раз, при этом никакие три или больше не встречались одновременно. Докажите, что до полудня у каждого велосипедиста было не менее n² встреч.
Решение
Пусть S – длина трека, v1 < v2 < ... < v2n – скорости велосипедистов, u = min {v2 – v1, v3 – v2, ...,
v2n – v2n–1}. Велосипедисты с номерами i < j встречаются через промежутки времени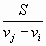 
.
Ясно, что самый большой из промежутков равен S/u, и нам придётся ждать до конца этого промежутка, чтобы каждый встретился со всеми остальными. Поскольку vj – vi ≥ (j – i)u, за это время велосипедисты с номерами i и j успеют встретиться не менее j – i раз. Значит, у n-го велосипедиста будет не менее 1 + 2 + ... + (n – 1) = ½ n(n – 1) встреч c теми, у кого номер меньше, и не менее 1 + 2 + ... + n = ½ n(n + 1) встреч – c теми, у кого больше. Итого не менее n² встреч. Для (n+1)-го оценка та же, а у остальных ещё больше.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь