Олимпиадная задача о пифагоровой таблице с цветной рамкой — 7-9 класс
Задача
В пифагоровой таблице умножения выделили прямоугольную рамку толщиной в одну клетку, причём каждая сторона рамки состоит из нечётного числа клеток. Клетки рамки поочередно раскрасили в два цвета – чёрный и белый. Докажите, что сумма чисел в чёрных клетках равна сумме чисел в белых клетках.
Пифагорова таблица умножения – это клетчатая таблица, в которой на пересечении m-й строки и n-го столбца стоит число mn (для любых натуральных m и n).
Решение
Решение 1:Пусть углы рамки чёрные. Каждое белое число рамки равно полусумме своих чёрных соседей по рамке, при этом каждое чёрное число входит в две полусуммы. Сложив эти равенства, получим, что сумма чисел, записанных в белых клетках, равна сумме чисел, записанных в чёрных клетках.
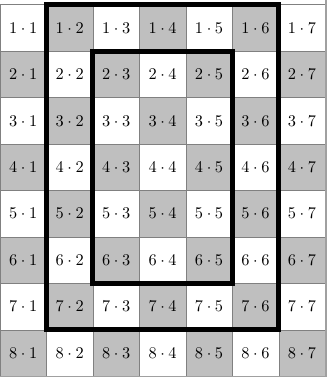
Решение 2:Продолжим шахматную раскраску на всю таблицу. Заметим, что среднее арифметическое чисел, стоящих в двух одноцветных клетках одного ряда (строки или столбца), равно числу в клетке, стоящей посередине между ними. Отсюда следует, что среднее арифметическое всех чисел, записанных в чёрных (белых) клетках рамки, равно числу, стоящему в центре рамки. Поскольку количество чёрных клеток в рамке равно количеству белых, то и суммы чисел, записанных в них, равны.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь