Олимпиадная задача по планиметрии: доказательство равенства дуг для 7–9 классов
Задача
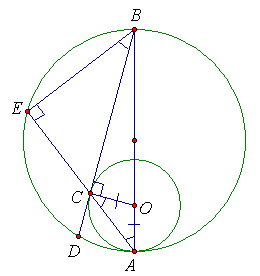
Даны две окружности, касающиеся друг друга внутренним образом в точке A); из точки B большей окружности, диаметрально противоположной точке A, проведена касательная BC к меньшей окружности. Прямые BC и AC пересекает большую окружность в точках D и E соответственно. Докажите, что дуги DE и BE равны.
Решение
Пусть O – центр малой окружности, ∠OAC = ∠OCA = α. Поскольку BC – касательная к малой окружности, то ∠BCO = 90°. Следовательно, ∠ACD = ∠BCE = 90° – α. Поскольку BA – диаметр большой окружности, то ∠BEA = 90°, откуда ∠EBD = 90° – (90° – α) = α. Поскольку вписанные углы EBD и EAB равны, то равны и дуги EB и ED.
Ответ
Ответ задачи отсутствует
Чтобы оставлять комментарии, войдите или зарегистрируйтесь
Комментариев нет